Objectives
The objectives of this section are:
to define agglomerative hierarchical clustering
to explain its basic algorithm
to briefly mention key issues it presents
Outcomes
By the time you have completed this section you will be able to:
define agglomerative hierarchical clustering
describe the algorithm
list key issues that this method creates/resolves
Initialization Step:
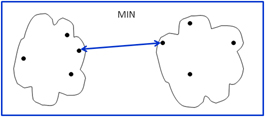
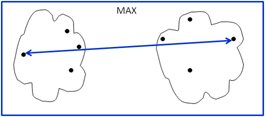
Proximity between clusters depends on the type of cluster one has chosen to use. If one decides to use a graph-based view of clusters then the agglomerative hierarchical clustering techniques that can be used would be the MIN, MAX and Group Average techniques.
MIN: this technique defines cluster proximity as the distance between the closest two points in different clusters as shown below. This technique works very well when it comes to recognizing non-elliptical shapes but it is sensitive to noise and outliers.
MAX: this technique defines cluster proximity as the distance between the farthest two points from different clusters. The advantage of this technique is that unlike the MIN approach it is less susceptible to noise and outliers. The downside is that it tends to break larger clusters and is biased towards globular clusters.
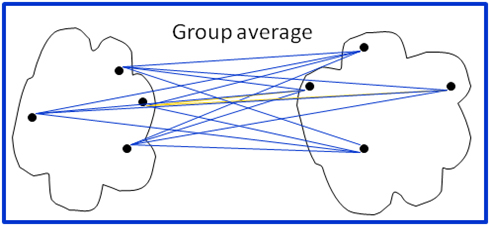
Group Average: defines cluster proximity as the average distance between points in one cluster to points in the second cluster. As one can see below in Figure 6, all points in cluster A are matched to points in cluster B and then later on the average is taken. This technique is a compromise between the MAX and MIN approaches its limitation is that it is biased towards globular clusters but is less sensitive to noise and outliers just like the MAX technique.
Other options include using a prototype-based cluster and some of the techniques that use this type of cluster include Cluster Centriods, and Ward’s method.
Merge Step:
After the proximity matrix is constructed, its values are used to decide which two clusters need to be joined together first. For instance, if we were to use the graph-based view of clusters and the MIN techniques, the two closest (minimum distance) clusters would be joined together.
Re-calculation Step:
The proximity matrix is updated to reflect the new clusters that have been constructed in the previous step. It is important to note that this re-calculation is heavily dependent on the clustering technique that has been used in the previous step.