Objectives
The objectives of this section are:
to explore training and testing errors and how they are influenced by the complexity of the tree.
to present the balancing act needed for an optimal decision tree.
to explain the concept of overfitting and underfitting.
to introduce you to the measure estimation of generalization errors.
to explore how overfitting is handle in decision tree induction algorithms.
Outcomes
By the time you have completed this section you will be able to:
to define training errors, testing errors, overfitting & underfitting.
to explain the balancing act needed to avoid either extreme.
to give a brief synopsis of the measures used to estimate generalization errors.
to explain how overfitting is handle in decision tree induction algorithms.
Measure Estimation of Generalization Errors
How do you figure out the right model complexity? Best case scenario is when you have the lowest generalization error, but this can’t be figured out because the learning algorithm only has access to the training set and so we don’t have a test set to help us evaluate how the model would respond to data it hasn’t seen before. The rest of this section presents various generalization error estimations
Using Resubstitution
This method assumes that the training set is a good representation of the overall data, so they use the training error and optimistically estimate that this value can be used to characterize the generalization error. This is a poor estimate.
Incorporating Model Complexity:
- Pessimistic Approach: In computer science being a pessimist is not consider a bad thing, preparing for the worst case scenario is sometimes a good rule of thumb. This model computes the generalization error as the sum of training error plus a penalty for model complexity. This is done because of Occam’s Razor which was previously discussed.
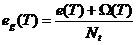
Where e(T) is the overall training error and Ω(T) is the total penalty associated for all the nodes.
- Minimum Description Length Principle: seeks a model that minimizes the overall cost function
INSERT EQUATION
Estimating Statistical Bounds:
The generalization error can also be estimated as a statistical correction to the training error. This correction is computed as an upper bound to the training error while taking into account the number of training records that reach a particular leaf node.
Using a Validation Set:
this method creates a test set but dividing the original training set into subsets using one to create the model and the only one to test the model.

